| Systems of Equations |
|---|
|
Two or more equations put together are called Systems of Equations. |
Below, we have a system of equations:
2y = x + 1
3x = 4y - 1
A solution to a system of equations is an ordered pair that works for every equation in the system.
Two methods for solving systems of equations are Graphing and Substitution.
First, we'll solve by graphing:
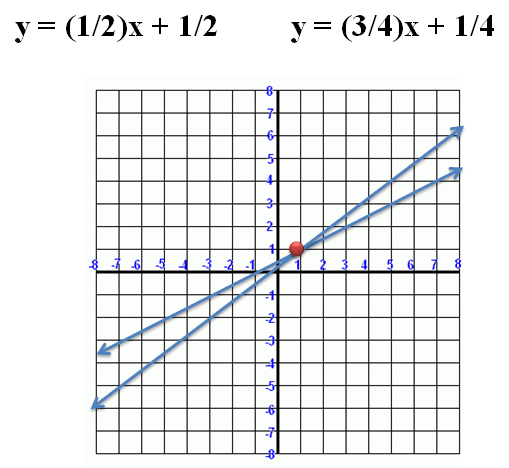
|
Figure 1. |
|---|
Above, we've written the two equations in slope-intercept form. We then graphed them, and found their intersection to be at (1, 1). Therefore, our solution is x = 1, and y = 1.
Next, we'll solve by substitution:
First, we solve the first equation for x:
x = 2y - 1
Now that we know what x is, we substitute it into the second equation:
3(2y - 1) = 4y - 1
6y - 3 = 4y - 1
2y - 3 = -1
2y = 2
y = 1
Now that we know what y is, we can plug it into the first equation to solve for x:
x = 2(1) - 1
x = 1
Thus, our solution is again (1, 1), where x = 1, and y = 1.