Post Hoc Tests for One-Way ANOVA (Jump to: Lecture | Video )

Remember that after rejecting the null hypothesis in an ANOVA, all you know is that the groups you compared are different in some way.

Imagine you performed the following experiment and ended up rejecting the null hypothesis:

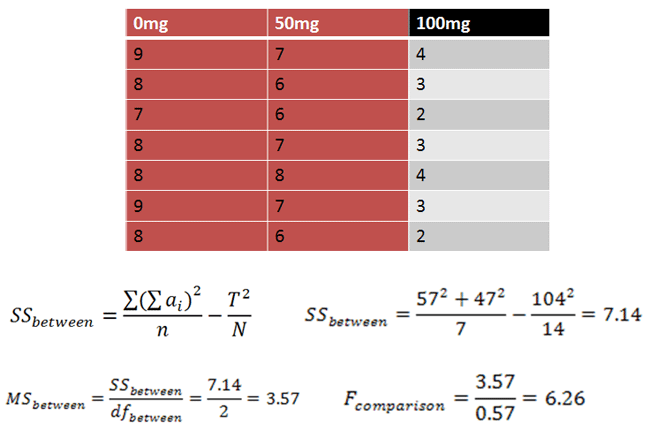
Researchers want to test a new anti-anxiety medication. They split participants into three conditions (0mg, 50mg, and 100mg), then ask them to rate their anxiety level on a scale of 1-10. Are there any differences between the three conditions using alpha = 0.05?

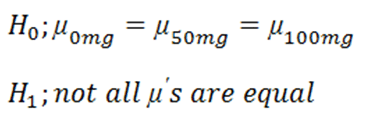
Figure 1.

Figure 2.

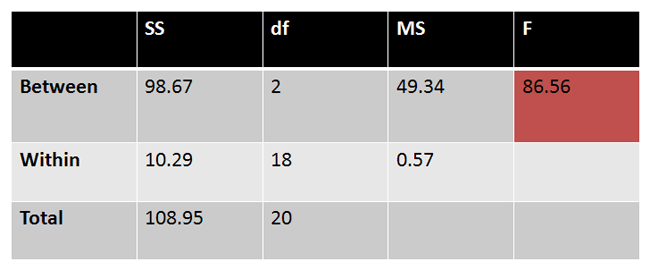
Now that we’ve rejected the null hypothesis, it is appropriate to perform a Post-Hoc test to discover where the three groups are different.

In this lecture, we'll be examining two different tests: Tukey HSD, and Scheffe.

The Tukey test is more liberal than the Scheffe test. When you perform a Tukey test, you have a greater chance of rejecting the null hypothesis, but you also have a greater chance of making a Type I error. With the Scheffe test you have less chance of rejecting the null hypothesis, but you also have less chance of making an error.

---

Tukey HSD

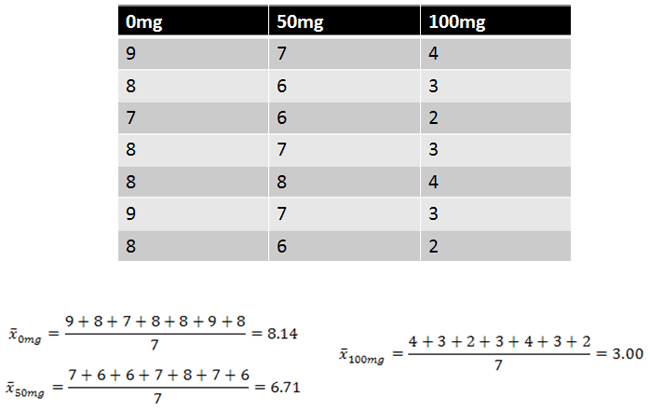
With this test, we’re interested in examining mean differences. So, we first calculate our means from our groups:

Figure 3.

Next, we calculate our HSD (Honestly Significant Difference) Figure 4.

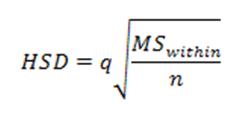
For this equation, we need MSwithin from our ANOVA source table, as well as our n. We also need a new statistic called "q". q is found in the q-table using our number of groups, and our number of degrees of freedom in the error term. We find a q value of 3.61 and put it into the equation to find our HSD.

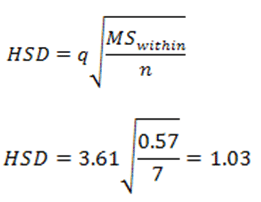
Figure 5.

Now, we measure how far each mean is from each other mean. Any means that are more than 1.03 apart can be considered different from each other:

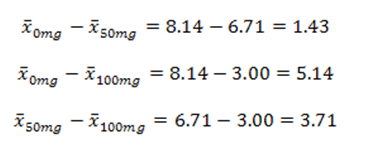
Figure 6.

Here, we find that all three means are different from one another.

---

Scheffe

In a Scheffe test, we calculate an F value for any pairwise or complex comparison we wish. Here's an F calculated for a comparison between the 0mg and 50mg groups:

Figure 7.

This new F is then evaluated using the decision rule from the original ANOVA:

If F is greater than 3.5546, reject the null hypothesis.

Reject the null hypothesis. The 0mg and 50mg groups differ from one another.

Now, try calculating your own F statistic for a different comparison.

---