Pascal’s Triangle (Jump to: Lecture | Video )

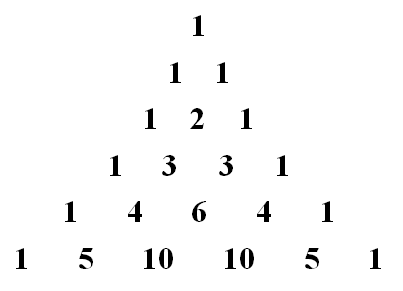
Figure 1.

Above, we have Pascal's Triangle. Moving downwards, each new term is the sum of the two terms directly above it.

Take the following expression, raised to the 5th power:

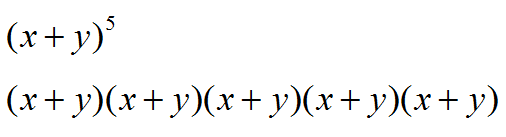
Figure 2.

The total expansion will have n + 1 terms, where n is equal to the degree (in this case, 5).

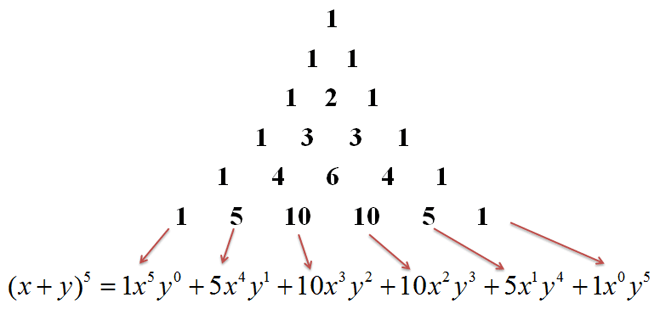
Figure 3.

The coefficients to our expansion are taken directly from Pascal's Triangle, saving us the work of finding them ourselves.

The exponents for our first variable start from our degree and descend to zero, while the exponents for our second variable start from 0 and ascend to our degree.

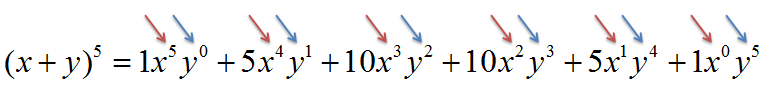
Figure 4.

Pascal’s triangle can be used to expand any similar binomial.