Multiplication Rule (Probability "and") (Jump to: Lecture | Video )

For example: rolling a five and then rolling a three with a normal six-sided die. These events are independent because rolling a five does not change the probability of rolling a three (it is still 1/6). The same is true the other way around.

What is the probability of rolling a 5 and then a 3 with a normal six-sided die? To answer this, we have the Multiplication Rule for Independent Events:

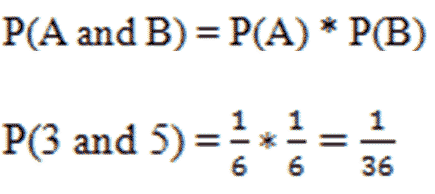
Figure 1.

There is a 1 in 36 chance of rolling and 5, and then rolling a 3.

For example: drawing a king and then drawing a queen from a deck of cards, without putting the king back. These events are dependent because drawing a king changes the probability of drawing a queen. Without the king in the deck the probability of drawing a queen changes from 4/52 to 4/51.

What is the probability of drawing a king and then drawing a queen from a deck of cards? To answer this, we have the General Multiplication Rule for Dependent/Conditional Events:

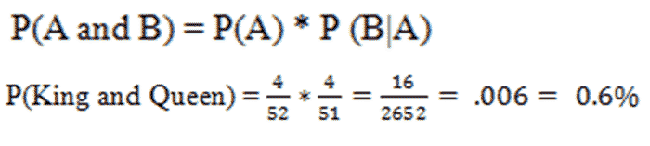
Figure 2.

There is roughly a 0.6% chance of drawing a king, and then drawing a queen without replacement from a deck of cards.