Equation of a Parabola (Jump to: Lecture | Video )

Figure 1.

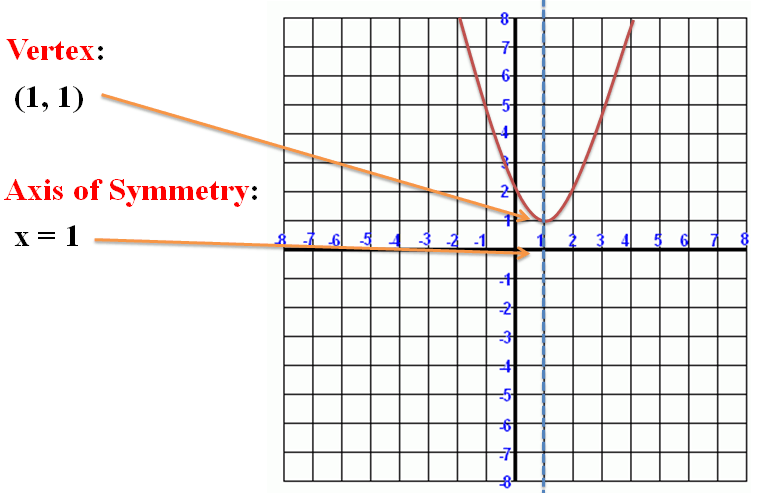
Above we have a parabola with its vertex and axis of symmetry labeled.

Equation of a Parabola
The standard form of an equation of a parabola with vertex (h, k) Axis of Symmetry x = h is written as: If a > 0, then k is the minimum, and the parabola opens upward. If a < 0, then k is the maximum, and the parabola opens downward.

Below, two parabolas are graphed:

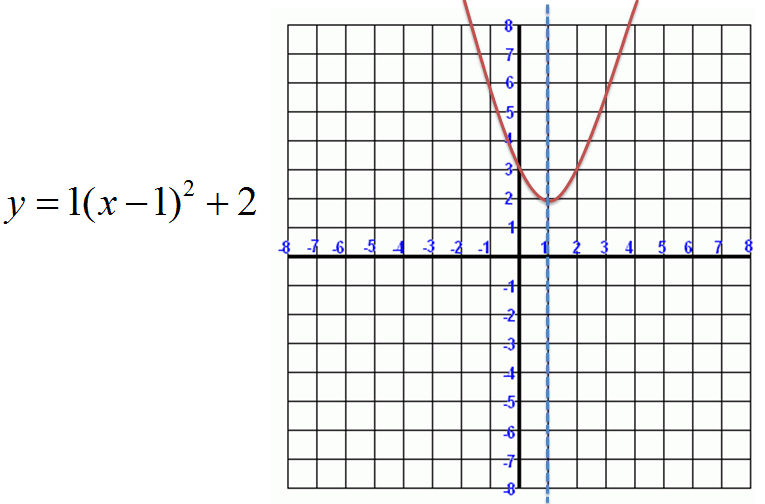
Figure 2.

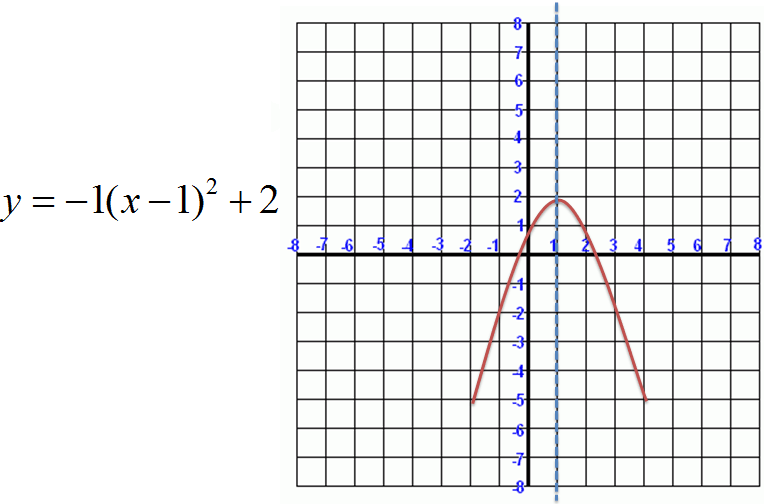
Figure 3.

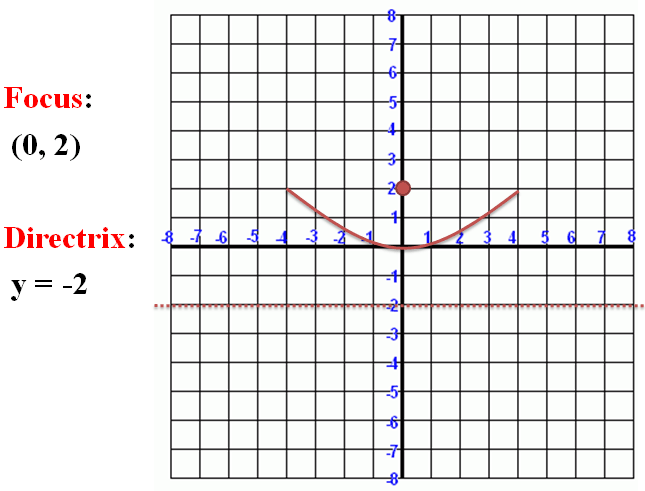
Each parabola has a focus, and a directrix.

Figure 4.

For any given point, the distance to the focus is equal to the distance to the directrix.

The Latus Rectum specifies the width of the parabola:

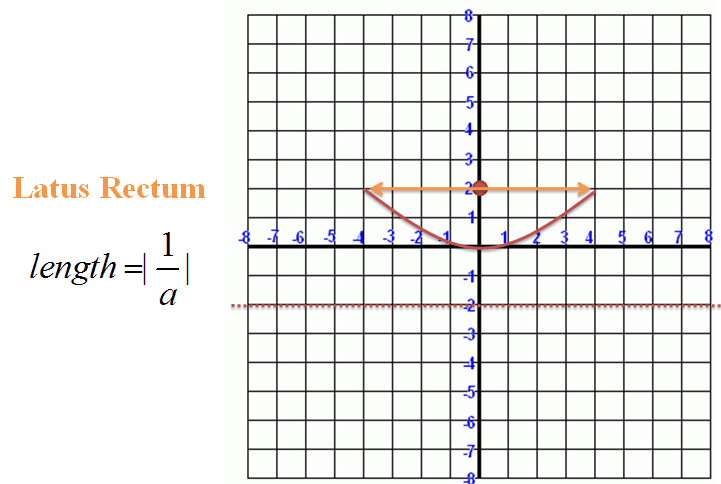
Figure 5.

The smaller a is, the wider the parabola is.