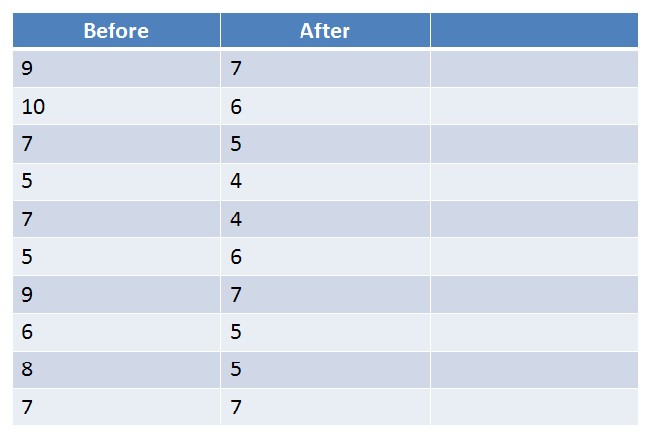
Let's perform a dependent samples t-test: Researchers want to test a new anti-hunger weight loss pill. They have 10 people rate their hunger both before and after taking the pill. Does the pill do anything? Use alpha = 0.05
|
Figure 1. |
|---|
| Steps for Dependent Samples t-Test |
|---|
|
1. Define Null and Alternative Hypotheses 2. State Alpha 3. Calculate Degrees of Freedom 4. State Decision Rule 5. Calculate Test Statistic 6. State Results 7. State Conclusion |
Let's begin.
1. Define Null and Alternative Hypotheses
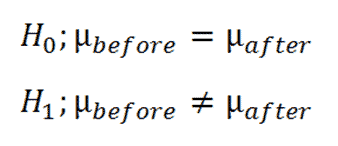
|
Figure 2. |
|---|
2. State Alpha
Alpha = 0.05
3. Calculate Degrees of Freedom

|
Figure 3. |
|---|
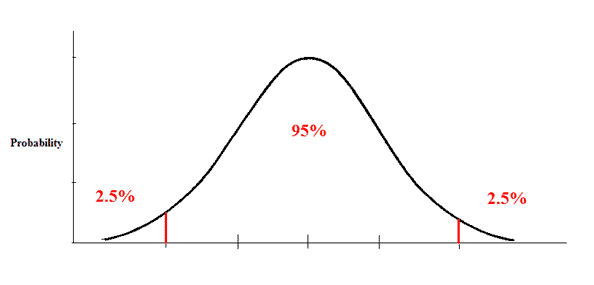
4. State Decision Rule
Using an alpha of 0.05 with a two-tailed test with 9 degrees of freedom, we would expect our distribution to look something like this:
|
Figure 4. |
|---|
Use the t-table to look up a two-tailed test with 9 degrees of freedom and an alpha of 0.05. We find a critical value of 2.2622. Thus, our decision rule for this two-tailed test is:
If t is less than -2.2622, or greater than 2.2622, reject the null hypothesis.
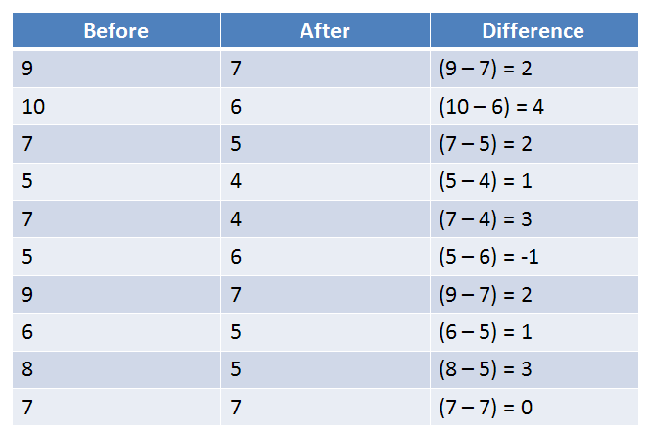
5. Calculate Test Statistic
The first step is for us to calculate the difference score for each pairing:
|
Figure 5. |
|---|
Now, we can calculate our t value:
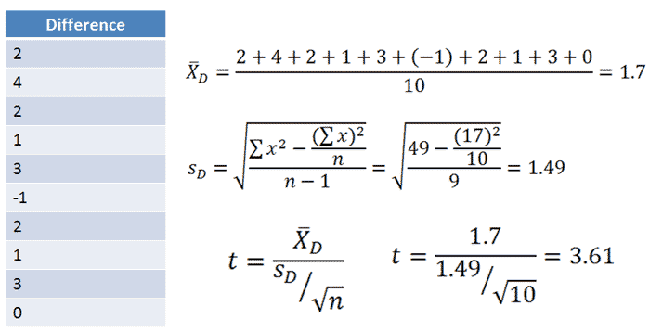
|
Figure 6. |
|---|
6. State Results
t = 3.61
Result: Reject the null hypothesis.
7. State Conclusion
The anti-hunger weight loss pill significantly affected hunger, t = 3.61, p < 0.05.