Combinations (Jump to: Lecture | Video )

Imagine you’re visiting a zoo with six animals, and I ask you to record the first three animals you see. The six animals are:

Tiger, Lion, Monkey, Zebra, Walrus, Snake

How many different combinations of three animals could you run into?

Figure 1.

There are 6 animals you could record in the first spot. After that, there are only 5 animals left to see for the second spot. And after that, there are only 4 animals left to see for the final spot. When we multiply those three numbers, we find that there are 120 different ways you could run into three different animals. Remember from the last lecture that this is a permutation.

When I say that there are 120 different ways you could run into three different animals, I'm saying that order matters. For example, there are six different ways to run into the same three animals:

Tiger, Lion, Monkey

Tiger, Monkey, Lion

Lion, Monkey, Tiger

Lion, Tiger, Monkey

Monkey, Lion, Tiger

Monkey, Tiger, Lion

In a combination, order does not matter. All six of those answers found above are really the same thing. So, there are 120 / 6 = 20 different combinations of animals that we could run into.

The combinations formula for our data would look something like this:

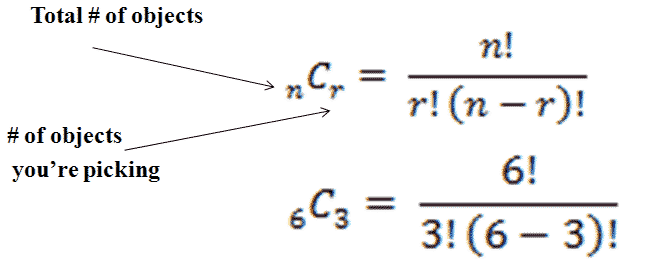
Figure 2.

But wait, what do the exclamation points(!) mean? Those mark factorials. Here are two examples of factorials:

6! = 6 * 5 * 4 * 3 * 2 * 1 = 720

4! = 4 * 3 * 2 * 1 = 24

In a factorial, you take the initial number and multiply it by every number between itself and one. So, our final answer for the first problem would look like this:

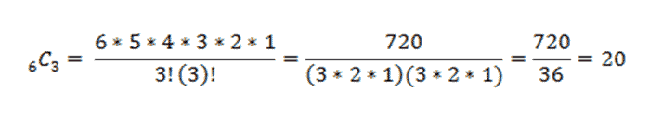
Figure 3.

As you can see, using the equation we still get an answer of 20.

---