|
Figure 1. |
|---|
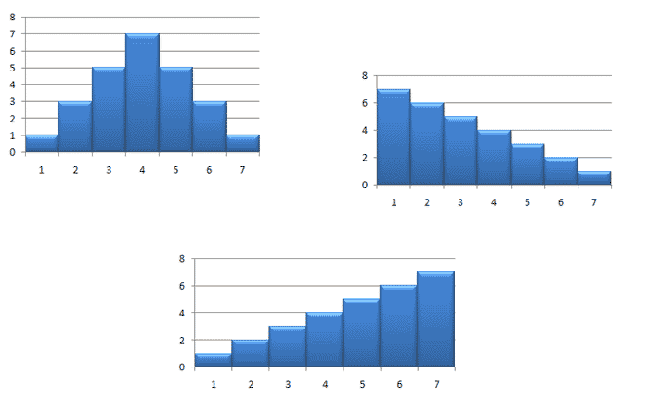
Here we have three different kinds of skewness. The distribution in the top left has no skew, the distribution in the top right is skewed right, and the distribution on the bottom is skewed left.
| The Central Limit Theorem |
|---|
|
The Central Limit Theorem states that regardless of the shape of the population distribution, the distribution of sample means will be approximately normal. |
From the central limit theorem, the following is true:
1. Population distributions that have no skew will lead to distributions of sample means that have no skew.
2. Population distributions that are skewed right will lead to distributions of sample means that have no skew.
3. Population distributions that are skewed left will lead to distributions of sample means that have no skew.
The distribution of sample means will become more normal as its sample size increases.
Good rule of thumb: sample distributions will usually be approximately normal if their sample size is n = 30 or larger.